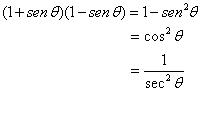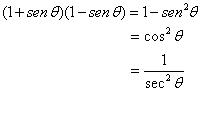Para establecer las razones trigonométricas, en cualquier triángulo rectángulo, es necesario conocer sus elementos.
Los ángulos con vértice en A y C son agudos, el ángulo con vértice en B es recto.
Este triángulo se caracteriza por que los lados de los ángulos agudos (α y γ)son la hipotenusa y un cateto, y los lados del ángulo recto (β) son los catetos.
Cada uno de los ángulos águdos del triángulo, uno de cuyos lados es la hipotenusa, se relaciona con los catetos, que pueden ser cateto opuesto al ángulo o cateto adyacente al ángulo.
Cateto adyacente es aquel que forma parte del ángulo al cual se hace referencia.
Cateto opuesto es el lado que no forma parte del ángulo que se toma como referencia y se encuentra enfrente de este.
razones o relaciones trigonométricas se establecen entre dos lados de un triángulo rectángulo en relación con cada uno de sus ángulos agudos. También se llaman Funciones trigonométricas.
Seis son las razones o funciones trigonométricas que se pueden establecer para cualquiera de los dos ángulos agudos en un triángulo rectángulo; de ellas, tres son fundamentales y tres son recíprocas.

Seno
Coseno

Tangente

Cosecante

Secante

Cotangente

(cateto contiguo o cateto adyacente)
APLICACIÓN DE LAS FUNCIONES TRIGONOMÉTRICAS
supongamos que queremos conocer el angulo de un triangulo rectangulo pero solo conocemos el cateto opuesto que vale 6 cm y la hipotenusa que tiene un valor de 9 lo que debemos hacer es
senA=co/ca
senA= 6/9
A=6/9/sen que es = A= sen-1(6/9)
como vemos aquí estamos aplicando SENO y como verán no es nada difícil lo mismo se hace con cada función; recuerden que la función a ocupar se escoge de acuerdo a los datos que nos proporciona el problema.
ANGULOS DE ELEVACIÓN Y DEPRESIÓN
Ángulos verticales
Estos ángulos están contenidos en un plano vertical.
Si se desea realizar alguna observación ya sea de objetos o puntos determinados del espacio, se utiliza dos términos muy comunes: ángulos de elevación y ángulo de depresión. Estos ángulos son formados por dos líneas imaginarias llamadas: línea visual o línea de visión y la línea horizontal. La línea de visión une el ojo de un observador con el lugar observado.
Ángulo de elevación
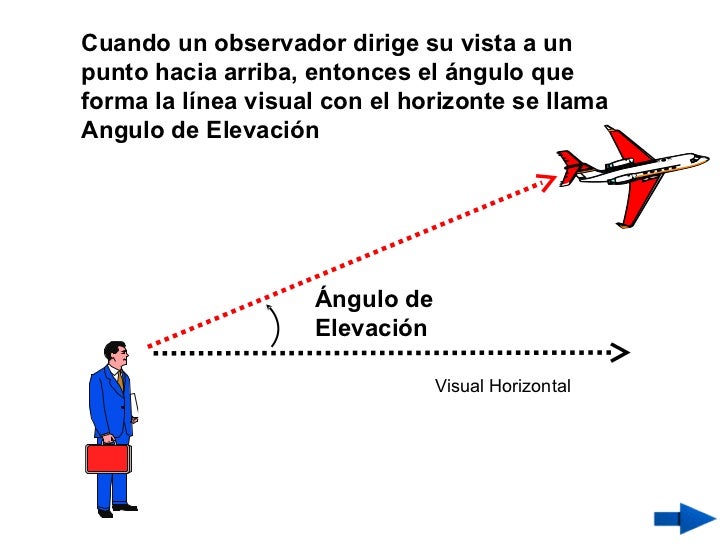 Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuando el objeto o punto observado se encuentra arriba de la línea horizontal.
Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuando el objeto o punto observado se encuentra arriba de la línea horizontal.
Ángulo de depresión
Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuan el objeto o punto observado está debajo de la línea horizontal.
Estos ángulos están contenidos en un plano vertical.
Si se desea realizar alguna observación ya sea de objetos o puntos determinados del espacio, se utiliza dos términos muy comunes: ángulos de elevación y ángulo de depresión. Estos ángulos son formados por dos líneas imaginarias llamadas: línea visual o línea de visión y la línea horizontal. La línea de visión une el ojo de un observador con el lugar observado.
Ángulo de elevación
 Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuando el objeto o punto observado se encuentra arriba de la línea horizontal.
Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuando el objeto o punto observado se encuentra arriba de la línea horizontal.Ángulo de depresión
Es el ángulo vertical (agudo) formado por la línea horizontal y la línea visual cuan el objeto o punto observado está debajo de la línea horizontal.

ÁNGULOS DE ELEVACIÓN DE SOL
como todos sabemos la tierra gira 360º por tal motivo el solo solo nos enfoca durante 180º para medir los ángulos de elevación del solo se ocupa un proceso muy sencillo solamente ocupando TANGENTE y un objeto.
primero medimos la altura del objeto, yo en este caso ocupe un palito de 16 cm que va a ser nuestro cateto opuesto,después lo ponemos en un lugar plano y medimos la sombra que produce en este caso 9.3 cm y ya tenemos aquí el cateto adyacente ahora ocupamos TANGENTE y listo.
ejemplo:
TAN <b = co/ca
TAN <b = 16/9.3
<b = 16/9.3/TAN
<b = TAN-1(16/9.3)
b = 59 º 49´57.74´´
IDENTIDADES TRIGONOMÉTRICAS
Las identidades trigonométricas son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Las siguientes identidades se cumplen
para cualquier ángulo en el cual el denominador no sea cero.
Estas son identidades recíprocas
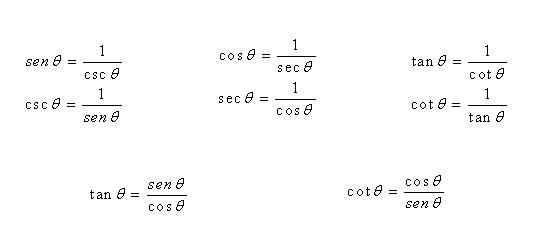
A partir de las relaciones pitagóricas es posible encontrar otras identidades y demostrar algunas identidades trigonométricas. Mediante estas relaciones si conocemos las medidas de los catetos de un triángulo rectángulo podemos calcular la medida de la hipotenusa (lado opuesto al ángulo recto) y si conocemos la medida de la hipotenusa y la de un cateto podemos calcular la medida del otro cateto. Entonces diremos que el teorema de Pitágoras es un teorema que se aplica únicamente a triángulos rectángulos, y nos sirve para obtener un lado o la hipotenusa de un triángulo, si es que se conocen los otros dos. Las identidades de relaciones pitagóricas son las siguientes:

De acuerdo al teorema de pitágoras :
Ahora veremos algunos ejemplos. Como primer ejemplo verificaremos la siguiente identidad:
Obtendremos la solución utilizando las identidades recíprocas:
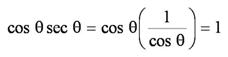
Observemos también el siguiente ejemplo, en el cual verificaremos otra identidad:
Su solución :